word
残存エラー率
（Residual Error Rate）
- 残存エラーというのは、情報を受けた側で、それが「間違いである」とわからないかもしれない確率のことです。これまでのメルマガをご覧になった方であれば、似たような話が出てきたと思います。そうです。故障率λ DU です。検知することができない通信データの間違い、それを残存エラーといいます。
- さて、なにかのデータ列があったとします。ここでは『ｎ』ビットあるとしましょう。そのデータ列が伝達されるときに、ノイズや機器の故障で変化したとします。つまり、０→１に変化したり、１→０に変化する場合を考えてみます。
- 実際の機器は電気信号ですから、途中で何らかの電気的なパルスや電磁波になるのですから、電気的な特性から、データ列の最初が間違いやすい、とか、データ列の特定の場所が変化しやすい、などの偏りがあるかもしれませんが、ここではビット列のすべてのビットの変化率、つまりエラー率が同じであるとします。その１ビット分の化ける確率をＰeとします。
- ある意味をもつ 『ｎ』ビットのビット列において、『k』ビット変化して違うビット列になる確率は、
- とあらわされます。これがぜんぜん意味の無いデータ列ならば、化けても困りません。意味不明のデータ、つまり「エラー」として受け手側で認識できます。しかしそれが別な意味をもつデータ列の場合、それはエラーとして受け手側で認識できません。つまり、間違って伝わってしまうことを意味します。
- そこで、あるデータ列の任意の『ｋ』ビットが変わることで、違う意味になるビット列の集合をＡ k とします。Ａ k は個数です。ある意味情報から、任意の『k』ビットが変化して得られるビット列のうち、別な意味を示すビット列の個数、といえます。
- このように考えると、変化するかもしれないビット数『k』の様々なケースを合計すると、ある『ｎ』ビットのデータ列のエラー率は、次のようにかけます。これが残存エラー率の計算の基本的な考え方の式になります。
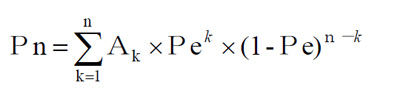
- とはいえ、Ａkを数えることはすごく大変です。そこで、前述の補足リンク①
で示す、CRCでのデータ空間の拡張を利用します。もともとの情報とビット列の表現に偏りがあったとしても、CRCコードをつける、つまりデータ空間を非常に大きく拡張することで、数学的に均質なデータの分布を考えることが出来る様になります。 - ではもう一度最初から、CRCコードでのデータ拡張を意識して考え直してみましょう。
- 『ｎ』ビットのうちの任意のどこかの『ｋ』ビット分が化ける確率は
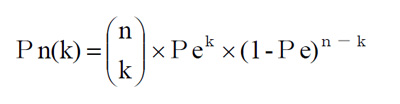
- ここでは、コンビネーション ｎＣk （『ｎ個』から『ｋ個』を取り出す場合の数）を、
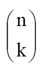と書くこととします。 - 『ｋ』ビットが変化するのですから、その確率はＰeの『ｋ』乗ですし、それ以外の『ｎ－ｋビット』は正しいのですから、その確率は（１－Pe）の『ｎ－ｋ』乗です。その変化が、どこかの『ｋ』ビットで起こるかもしれないということですから、その場合の数をぜ～んぶ合計すると、上のようになるわけです。
- この『ｋ』個のエラーが発生したという話、１個だけの場合もあれば、最悪は『ｎ』個に同時に発生するかもしれません。よって、あらゆるケースを想定した、データのエラー確率（Ｐ UL ）は、あらゆる『ｋ』の場合の可能性を合計することになりますから、
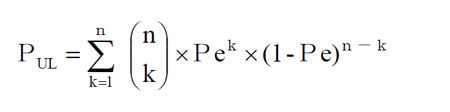
- となります。
- しかし実際のデータは、意味を持つ符号と、ビットの列の間の相関関係から、あらゆるビット列が意味を持つとは限りません。これは前述したとおりですね。化けても意味を持たないビット列ならば、それはエラーとして認識できます。
- 例えば、２つの符号Ａ，Ｂしかない世界の場合、それを1111と0000として表すとすると、その他の1001や0110は、意味のない情報となります。そんなデータがきたら、受け手側で『エラーである』ことがわかりますね。つまりこのような場合は、検知できるのですから、『残存エラー』とは呼べません。
- そこで、この意味のある情報と、意味のある情報の間の遠さ近さを表す数字として、Hamming（ハミング）距離（＝ｄ）というものが考えられました。Hammingさんが考えたものです。
- Hamming距離が１つまり ｄ＝１とは、1ビット化けるだけで、別な意味のある情報に変化する場合を表すとします。先ほどの符号が1111と0000しかないケースでは、d=4となります。4ビット変化したら、意味のある別な情報に変ってしまうからです。
- これを考慮して、先ほどの式を利用して、間違ったことがわからない場合の確率、つまり残存エラー率（Ｒ UL ）を式にするとどうなるでしょうか。
- ｄビット未満の変化は、「エラーだ」とわかるのですから、検知できないエラーとしてカウントするべきなのは、ｋ＝１からではなくて、ｋ＝ｄ からとなります。
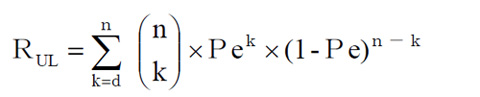
- と表されます。これが残存エラーと言ってよさそうです。
- しかし現実にはこれも使えない式です。実際にはパリティ（データ列の各ビットの合計が偶数か、奇数かの判定情報を付加する処理）をつけたような場合、いわばそれはHamming距離ｄ＝２と言えます。２ビット化けるとわからなくなるからです。しかし、それは１ビット化けの場合だけではなく３ビット化けも検知できます。そうなると、上の式は、単にｄ＝２からのケースを全部合計すればよい、と単純に合計するわけにはいきませんよね。足しすぎます。
- このようなちょっとした工夫をするだけで、上の式は使えなくなります。現実には通信には様々な冗長符号を付加し、エラーの検知ができるような工夫をしますから、残念ながらこの式は、残存エラー率の算出には使えません。（使えないのに何故書いたかというと、あとで判ります。）
- ではどうすればいいのでしょうか。
- 上の式が使えないのは、式の中に符号（意味のある情報）の分布についての要素が全く入っていないからです。意味のある情報が、どの程度バラけているのか、それによって変化したビットによって、それがエラーとして検知できるのか、検知できないのか変わってくるのです。ここで、補足リンク①のCRCを思い出しましょう。データ空間の拡張を活用します。
- CRCを付加することを考えると、『ｒ』ビットの冗長ビットをつけたメッセージは、情報のバラけ方が、『２ ｒ 』倍になっています。
- もともとのメッセージの意味空間のバラけ方はこの際考えなくても、『ｒ』ビットのCRCをつけることによって、少なくとも均等に意味の有るメッセージが、別な意味のあるメッセージに変化する確率は、『２ ｒ 』だけ小さくなっている（薄まっている）といえます。
- このことにより、『ｒ』ビットの冗長符号をつけた場合は、前述の式は、
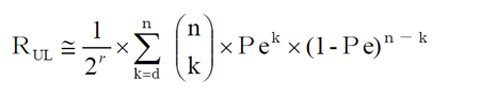
- と考えることが適切であるといえます。
- Ｐを極めて小さな数として考えると、この式は、最初の第一項を展開したものを用いて、下記のように書き換えることが出来ます。
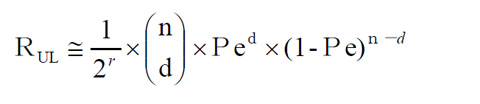
- つまり残存エラー率は、おおよそHamming距離と冗長ビット長の関数として表されるのです。